[e]Motion &vectors
tutorial de programmation du mouvement en processing	Nicolas Schöffer, Tour cybernétique 1956

Le mouvement dans l'art

L’introduction du mouvement

Les intentions qui conduisent les artistes à introduire le mouvement dans leurs œuvres sont souvent divergentes.

Dès 1909, certains artistes – tel le futuriste italien Umberto Boccioni – font de la vitesse et du mouvement mécanique un idéal esthétique et moral, mettant en branle une réalité jusqu’alors tenue pour stable et immuable et démolissant les représentations de l’ancien monde. D’autres, plus proche du cubisme, s’intéressent au caractère mouvant de la perception, à la simultanéité des points de vue qui se conjuguent au sein de représentations mentales : assemblages précaires pour les uns, sublimations pour les autres. Ils développent ainsi la vision d’un réel multiple et insaisissable.

Référence

Un bon article sur l'histoire du mouvement dans l'art >>

Film expérimental, expanded Cinema, calculated Cinema

Oskar Fichinger ( Studio N° 6+ 7, 1930,31)

Norman McLaren (film sans caméra ni appareil d'enregistrement )

Hans Richter Rythmus 21, 1921

Walter Ruttmann Opus IV 1925

John Whitney Matrix III 1972

Lary Cuba "Calculated Movements"

http://archive.constantvzw.org/events/vj5/progF.html#con

Sculpture cinétique:

Moholy Nagy:Lichtmodulator

Marcel Duchamps Anemic Cinema

Julio Le Parc

Son et lumière

Son et lumière: Catalogue du Centre Pompidou 2004

Force & Newton

http://fr.vikidia.org/wiki/Lois_du_mouvement_de_Newton

Ce tutorial introduit des notions de base pour programmer le mouvement dans Processing. Au même temps, le cours introduit une nouveau type d'objet, le vecteur, qui nous permet de décrire une point et son déplacement dans un espace 2D ou 3D. Comme la déscription du mouvement est une discipline de la physique, nous aborderons également quelques terminologies fondamentaux en physique ou plus précisément la cinématique, la science qui décrit le mouvement des objets.
Ce tutorial est basée sur un tutorial de modèle physique en Lingo, au cours en ligne de physique et le tutorial de Shiffman sur les vecteurs sur le site de processing ainsi que le chapitre "Motion" du livre Mathematics for programmers.

Vecteur et vélocité

D’abord clarifions la terminologie qui est utilisé pour décrire le mouvement en physique :
Le mouvement est décrit par ces deux quantités mathématiques distinctes vectorielle ou scalaire :
Vélocité, (Velocity) quantité vectorielle, » le taux auquel un objet change sa position »
Vitesse (Speed) quantité scalaire, « un objet bouge combien vite».

Pour comprendre la différence, imaginons quelqu'un’un qui se déplace d’un pas avant d’un pas en arrière. Sa vélocité est égal 0, mais sa vitesse n’est le pas. La vélocité est donc une quantité vectorielle, elle est liée à la direction. Il ne suffit pas de dire que la vélocité d’un objet est 20m/min, il faut dire 20m/min en direction nord par exemple.
La vitesse ne prend pas en considération la direction, elle mesure juste la distance qu’un objet a parcourue dans un temps donnée. La personne qui a fait quatre pas avant et quatre pas en arrière a parcourue une distance de 8 pas, mais zéro pas de déplacement. Le déplacement est une quantité vectorielle et donc liée à la vélocité, la distance est une quantité scalaire est donc lié à la vitesse.
Le scalaire est une quantité qui est décrit seulement par une grandeur (or valeur numérique).
Le vecteur est une quantité décrite par une grandeur et une direction.

 

Vecteur versus coordonnées( x,y)

Alors pour décrire une mouvement dans un espace, on peut utiliser des vecteurs. On n'est bien sure pas obligé, on peut très bien le faire comme on l'a fait juste à présent.

float x = 7, y = 3;
float x_vitesse = 2, y_vitesse = 5;
....
x+= x_vitesse;
y+=y_vitesse;
etc..

Mais imaginons on a pour chaque propriété une seule variable qui décrit la position (x, y) et la vélocité (x_vitesse, y_vitesse). Exact, c'est ça un vecteur. Processing à sa propre classe, qui s'appelle PVector. Regardons le pseudo code ci-dessous:

PVector position;
Pvector velocite;
...
position += velocite;
etc...

Ce code à l'aire plus simple que le précédent, mais évidement, pour se simplifier la vie, il faut d'abord passer par quelques complications. Commençons simple, c'est quoi exactement un vecteur?

Vecteur

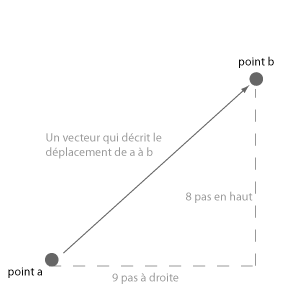
Un vecteur est une collection des valeurs qui décrivent une position relative dans l'espace et nous permet également de décrire son déplacement.

On pourrait objecter qu'il y a une différence entre une position et une déplacement, mais on verra aussi qu'on peut négliger la différence. En effet, le point décrit la différence entre le point d'origine et sa position et le vecteur de déplacement décrit celle de a à b.

PVecteur class dans Processing

Si on ouvrirait le code source de Processing pour regarder comment la classe des Vecteurs est implémenté, on trouvera +/- le code suivant (voici juste le début

class PVector {
float x, float y;
PVector (float x_, float y_){
x=x_;
y=y_;
}
}...

En gros, la classe PVector permet de stocker des positions des points. A place de décrire la position et la vitesse par coordonnées et addition d'un distance, on pourrait additionner directement des vecteurs. Regardons comment l'addition des vecteurs fonctionne:

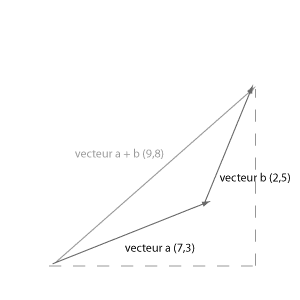
En effet, on addition les deux composant des deux vecteurs, ce qui donnera en terme de la classe Vecteurs

class PVector {
float x, float y;
PVector (float x_, float y_){
x=x_;
y=y_;
}

void add(PVector a){
x = a.x;
y = a.y;
}
}...

Au lieu décrire la position += velocite, on utilise la fonction de la classe add()

PVector position;
PVector velocite;

void setup(){
position = new PVector(7,3).
velocite = new PVector(2,5);
}
void draw(){
position.add(velocite);
}

Ensuite if faut renseigner la position à une forme, par exemple une ellipse. Comme elle n'accepte pas un vecteur comme argument, il faut découper à nouveau le vecteur en ces composants x, y

ellipse (position.x, position.y, 10, 10);

 

Algèbre des vecteurs

Pour l'instant, nous n'avons pas gagné grand chose avec les vecteurs. Mais nous n'avons pas non plus exploiter toute les capacités de la class PVector. Si on fait un tour sur le page des Vecteurs dans Processing, nous remarquons qu'il y a un tas d'autres fonctions qui appartient à la class PVector.

add()	Adds one vector to another
sub()	Subtracts one vector from another
mult()	Multiplies the vector by a scalar
mag()	Calculate the magnitude (length) of the vector
div()	Divides the vector by a scalar
dist()	Calculate the Euclidean distance between two points
dot()	Calculates the dot product
cross()	Calculates the cross product
normalize()	Normalizes the vector
limit()	Limits the magnitude of the vector
angleBetween()	Calculates the angle between two vectors

Vector substraction

Nous allons discuter rapidement ces différents méthodes et les concepts mathématiques qui sont derrière.

La méthode substraction fonctionne de la même manière que celui de l'addition. Graphiquement, cela ressemble à ça.

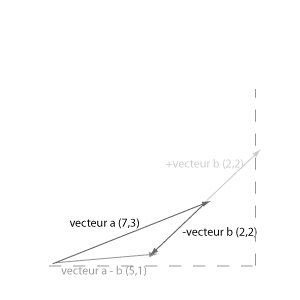
Voici un petit code qui montre le principe de l'addition et substraction du vecteur. Il faut rapidement cliqué, sinon le Vecteur part dans la nature:

PVector pos;
PVector vel;
PVector buf;

void setup() {
size(300, 300);
pos = new PVector (width/2, height/2);
vel = new PVector (2, 2);
buf = pos.get();
}

void draw() {
background(255);
if (mousePressed)pos.sub(vel);
else pos.add(vel);
line(pos.x, pos.y, buf.x, buf.y);
buf = pos.get();
}

Multiplication et division avec les Vecteurs

Si on parle de multiplier un vecteur, on entend mettre à l'échelle un vecteur. Si on veut avoir le double d'un vecteur ou un tiers d'un vecteurs, on multiplie le vecteurs par deux ou on le divise par 3. En effet, on ne multiplie pas un vecteur par un autre (ce qu'on appelle le dot product, qui nous intéresse pour l'instant pas) mais avec un scalaire.

Les méthodes à l'interieur de la class PVector ressemble un peu près à ça.

void mult(float scalaire){
x = x*scalaire;
y = y*scalaire;
}

void div(float scalaire){
x = x/scalaire;
y = y/scalaire;
}

Et voici la petite démonstration de ces calcules.

PVector pos;
PVector vel;
PVector buf;
float scalaire =1.2;
void setup() {
 size(300, 300);
 pos = new PVector (width/2, height/2);
 vel = new PVector (2, 2);
 buf = pos.get(); strokeWeight(3);
   }
void draw() {
 background(255);
 if (mousePressed)pos.sub(vel);
 else pos.add(vel);
 line(pos.x, pos.y, buf.x, buf.y);
   buf = pos.get();
   }
 void keyReleased(){
 if (key=='m') vel.mult(scalaire); if (key=='d') vel.div(scalaire);
   }
   

Magnitude /normalize

Un vecteur comporte deux informations, une direction et une longueur. Il est souvent pratique de connaître ces deux informations d'une manière indépendant. Imaginons, on a un vecteur de vent, et on veut savoir sa direction et sa force. Commençons avec la longueur du vecteur

 

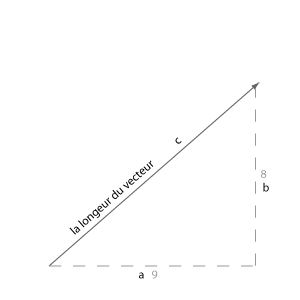
Si on regarde bien, on voit un triangle, qui se forme par x(marqué a), y (marqué b) et la longueur (marqué c). Finalement, il est simple de calculer la longueur avec la formule de Pythagore a² +b²=c² ou bien
c=racine( a² +b²), la méthode ressemble à ça:

float mag(){
return sqrt(x*x+y*y);
}

Sa direction est à priori une proportion entre sa direction verticale et horizontale. Pour exprimer ceci, il sera d'avantage de le faire sans que le vecteur à une longueur particulier, ou bien il faut le normaliser, standardiser. Si on met la longueur à 1, on peut par exemple comparer l'orientation avec n'import quel autre vecteur standardisé. Ce vecteur normalisé s'appelle vecteur unitaire. Pour ce faire il faut simplement agrandir, ou rétrécir notre triangle à fin que l'hypothenuse devient 1.

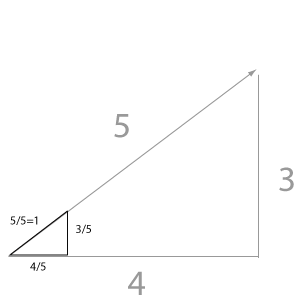
En gros l'opération est de diviser le Vecteur par sa magnitude. Voici la méthode de la classe Vecteur

void normalize(){
float m = mag();
div(m);
}

Nous utilisons la fonction normalize() dans le code suivant à fin d'indiquer la direction de la velocité. Pour l'instant nous avons changé la direction par l'addition ou la substraction à la position. Mais en effet, la vélocité elle même change pas. Dans ce code, nous modifiant la direction en multipliant la vélocité par -1. Ensuite, nous passons ce vecteur à un nouveau vecteur 'dir' pour pouvoir le manipuler indépendamment. Nous calculant son vecteur unitaire et multipliant par 20 pour le rendre visible.

Utilise la touche c = changer direction, m = multiplier

PVector pos;
PVector vel;
PVector buf;
PVector dir;
float scalaire =1.02;

void setup() {
size(300, 300);
pos = new PVector (width/2, height/2);
vel = new PVector (0.5, 0.5);
buf = pos.get();
smooth();
}
void draw() {
background(255);
pos.add(vel);
strokeWeight(3); 
line(pos.x, pos.y, buf.x, buf.y);
buf = pos.get();// pour garder dans la mémoire la position précédente
// calcule et desssine la longueur de velocité
float longueur = vel.mag();
fill(255, 0, 0);
rect(0, height-longueur*50, 10, height);
dir = vel.get();
dir.normalize();
dir.mult(20); 
fleche(dir);
}

void fleche(PVector f) {
pushMatrix();
noFill();
strokeWeight(1);
translate(width/2, height/2);
line(0, 0, f.x, f.y);
ellipse( f.x, f.y, 5, 5);
popMatrix();
}

void keyReleased() {
if (key=='m') vel.mult(scalaire);
if (key=='c') vel.mult(-1);
if (key=='d') vel.div(scalaire);
}

 

limite

Il est souvent judicieux de limiter des vecteurs comme la vélocité par un valeur maximale. Dans ce cas, il s'agit évidement de sa magnitude. On regardant le source code, on voit que le vecteur unitaire nous sert aussi dans ce cas.

void limit(float max) {
if (mag() > max) {
normalize();
mult(max);
}
}

========================================================================

Force & Newton

Nous allons utiliser maintenant les vecteurs et ses fonctions pour développer une classe d'un objet qui à son tour a des méthodes des principaux mouvements (accélération, friction, gravité....) D'abord nous étudions les loi de Newton, qui nous permettrons ensuite de comprendre le comportement cinétique des objets.

Les trois lois de Newton, lois de la dynamique ou lois du mouvement sont des principe de base décrivant le mouvement des objets. Elles ont été énoncées par Isaac Newton au XVIIe siècle.

Première loi - principe d'intertie

« Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n'agisse sur lui, et ne le contraigne à changer d'état. »

Deuxième loi - principe fondamental de la dynamique

Soit un corps de masse m (constante) : l'accélération subie par ce corps est proportionnelle à la résultante des forces qu'il subit, et inversement proportionnelle à sa masse m.

Troisième Loi -principe des actions réciproques

« Tout corps A exerçant une force sur un corps B subit une force d'intensité égale, de même direction mais de sens opposé, exercée par le corps B »

 

classe Objet

D'abord nous écrivons la classe de notre objet qui a comme propriété une position, vélocité, accélération qui sont des vecteurs, et une masse, comme grandeur scalaire. Les méthodes sont update, draw, et border pour faire rebondir les objets aux bords du sketch. Pour l'instant la vélocité est un force donnée, qui ne résulte pas pour l'instant d'une force extérieure, donc en ignore dans un premier temps la masse aussi.

 

class Objet {
  PVector pos;
  PVector vel;
  PVector acc;
  float masse;

  Objet (PVector p, PVector v, PVector a, float m) {
    pos = p.get();
    vel = v.get();
    acc = a.get();
    masse = m;
  }

  void update() {
    border();
    vel.add(acc);
    pos.add(vel);
    acc.mult(0);
  }

  void draw() {
    update();
    fill(255);
    ellipse (pos.x, pos.y, masse*5, masse*5);// *5 pour le rendre un peu plus grand
  }
  void border() {
    if (pos.x <0) {
      pos.x = 0;
      vel.x*=-1;
    }
    if ( pos.x > width) {
      pos.x = width;
      vel.x*=-1;
    }
    if (pos.y <0) {
      pos.y = 0;
      vel.y*=-1;
    }
    if ( pos.y > height) {
      pos.y = height;
      vel.y*=-1;
    }
  }
}

Et nous allons implementer cette classe dans un code simple

Objet objet;

void setup() {
  size(300, 300);
  objet = new Objet(new PVector(width/2, height/2), new PVector(0, 0),
  new PVector ( random(-1, 1), random(-1, 1) ), random(5, 10));
}

void draw() {
background(0);
 objet.draw();
}

}

 

Forces

Revenons à Newton pour comprendre le rapport entre mouvement, masse et force. Ce qui nous intéresse tout particulièrement, c'est sa deuxième loi, le rapport entre la masse d'un objet et l'accéleration:

force = masse * accélération

Pour calculer l' accélération, nous inversons l'equation: accélération = force / masse.

Force
Dans le monde physique, l’accélération est le résultat d’une force par exemple la gravité, le vent, la friction... L'accélération est la somme de toute ses forces. Selon la formule de Newton, il faut donc diviser la force par la masse du objet et ensuite l'additionner à l'accélération. Si on traduite cela en code, ça donnera la méthode suivante, qu'on rajoute à notre class Objet:

void appliqueForce(PVector force) {
  force.div(masse);   
  acc.add(force); 
}

Imaginons nous avons une force de gravité (ou moins une simplification de celci, une force vers le sol) et une vent venant de l'ouest.

PVector gravite = new PVector(0, 0.4);
PVector vent = new PVector ( 0.1, 0);

Nous allons implementer ce deux forces dans notre code principale en mettant l'accélération initiale à 0 et en rajoutant la méthode appliqueForce(PVector force) dans la class Objet;

Objet objet;

void setup() {
  size(300, 300);
  PVector pos = new PVector(width/2, height/2); 
  PVector vel = new PVector(0, 0);
  PVector acc =new PVector(0, 0);
  objet = new Objet(pos, vel, acc, 1.5);
}

void draw() {
  background(0);
  objet.draw();
  PVector gravite = new PVector(0, 0.08); 
  objet.appliqueForce(gravite);
  PVector vent = new PVector ( 0.01, 0);
  objet.appliqueForce(vent);
}

Pour l'instant l'objet rebondit sans arrêt. Mais pourquoi?

La vélocité augmente progressivement en additionnant les forces exercés, en arrivant au sol, le ballon a une vélocité disons de 10. Quand le ball rebondit, la vélocité devient négative (-10) mais continue a additionner la 'force gravitionnel' (+0.08) elle s'approche du zéro jusqu'au point de départ et redevient à ce moment positive.

L'algorithme n'est pas très crédible comme simulation. Ceci est lié à 2 choses, d'une part, l'élacticté de l'objet est actuellement égal 1, ce qui s'exprime dans le code par la multiplication par -1 lorsque l'objet touche le sol. On pourrait rendre l'objet 'moins élastique en changeant cette valeur en -0.7 par exemple. Mais pour continuons avec les forces, nous allons rajouter une autre force, celui de la friction de l'aire.

sd

Friction / Viscosité

Il y a deux forces dissipatif, la friction et la viscosité.

La friction s’applique entre deux corps, un carton par terre qu'on veut pousser par exemple. La viscosité s'applique quand un objet travers une gaz ou une fluide, on sent cette force quand on est sur un vélo ou sur un moto. D'une manière générale, contrairement à la gravité de l’exemple précédent qui agit vers le bas, la friction d’aire agit toujours dans la direction opposée de la vélocité. La friction est indépendant de la vélocité, par contre la viscosité augmente avec la vélocité. La formule pour l'un et l'autre est, avec c pour le coefficient de la friction/ viscosité :

force de friction = -c * vecteur unitaire de vélocité

force de viscosité = -c * vecteur de vélocité

Comment alors exprimer ceci en code ?

  void appliqueViscositeForce(float c) {
    c*=-1;
    PVector viscositeForce = PVector.mult(vel, c);
    appliqueForce(viscositeForce);
  }

et on l'utilise par exemple comme ceci dans le code principal:

  if (objet.pos.y > 200 && objet.pos.y < 240) {
    objet.appliqueViscositeForce(0.1);
  }
  fill(255, 80);
  rect(0, 200, width, 40);// liquid visceux
...

 

Force gravitationnelle

La gravitation est le phénomène d'interaction physique qui cause l'attraction réciproque (3ème de Newton) des corps massifs entre eux, sous l'effet de leur masse. La formule est

(G * Masse1*Masse2)/ distance*distance

G est la constante gravitationnelle, qu'on peut ignorer dans la simulation.

Enfin de calculer la Gravitation entre deux corps, nous pouvons calculer la magnitude du vecteur entre les deux corps. Pour calculer la direction, nous prenons le vecteur unitaire de celui-ci. Ensuite on applique l'équation de Newton et multipliant le résultat avec le vecteur unitaire.

PVector direction = PVector.sub(vec1.pos, vec2.pos);
float distance = direction.mag();
direction.normalize();
float force = (G * Masse1*Masse2)/ distance*distance
direction.mult(force);

Traduirons ceci en code pour notre class Objet avec la méthode constraint pour limiter des chiffres trop grand ou petit.:

  PVector getGraviteForce (Objet obj) {
    PVector direction = PVector.sub(pos, obj.pos); 
    float distance = direction.mag();
    distance = constrain(distance,5.0,25.0); 
    direction.normalize();
    float force = (G * masse * obj.masse)/ (distance*distance);
    direction.mult(force); 
    return direction;
  }

et pour le code principale ou seulement le Objet du centre exerce une force de gravité

Objet objet;
Objet objetCentre;
void setup() {
  size(300, 300);
  PVector pos = new PVector(width/2, height/2); 
  PVector vel = new PVector(0, 0);
  PVector acc =new PVector(0, 0);
  objetCentre = new Objet(pos, vel, acc, 20);
  
  pos = new PVector(50, 50); 
  vel =  new PVector(0, 1);
  objet = new Objet(pos, vel, acc, 10);
}

void draw() {
  background(0);
  PVector grav = objetCentre.getGraviteForce(objet);
  objet.appliqueForce(grav);
  objet.draw();
  objetCentre.draw();
}

Force d'élasticité (Spring force)

Dans l’exemple suivant, on simule un ballon élastique qui rebond sur un surface.
L’idée est que le ballon, le moment qu’il touche le sol, se contracte et « se charge » en force élastique. De plus le ballon s’écrase, donc la distance entre sol et le point de référence (y1) diminue, la force élastique augmente ; elle est égale à la distance entre y1  et y2, est opposé à sa force d’origine (la gravité).

 

 

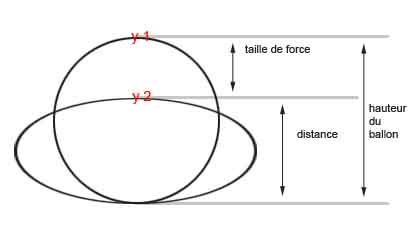
Ce qu'il faut connaître:

• le vecteur et son arithmétique
• les lois de Newton
• les forces principales

 

Exercice