Triangle etCercle tutorial de programmation en processing
	moving lines

 

Le cours

Le cours aborde d'abord quelques notions fondamentale de la trigonométrie qu'on va ensuite appliquer dans des algorithmes génératives.

Trigonométrie

Pour certain, le mot trigonométrie évoque seulement de mauvaise souvenir de l'école, ce que je comprends mais j'espère aussi de démontrer que quelques connaissance en trigonométrie 'sont très utile dans la programmation, et ça peut être même fascinant.

Jusqu'aà présent, les animations ont été assez carré, on sait bouger des objets sur un ligne, on se dessiné des formes géometriques primitifs, la vitesse est regulier etc. Avec quelques notions de trigonométrie, les lignes peuvent se courbé, les objets peuvent prendre des chemins en serpent, ils peuvent accèlerer d'une manière progressives. Avec quelques connaissance en math, nous gagnerons en liberté dans les animations.

La distance

Dans un premier temps, nous utilisons la trigonométrie pour calculer la distance entre deux points dans l'espace. Si nous lierons deux points par un ligne, nous pouvons formé un triangle avec les distances qui séparent les deux point x et les deux points y.

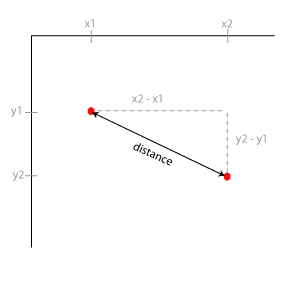
Selon le théorème de Pythagore, dans un triangle la coté le plus longue (l'hypothenuse) en carré est égale au deux autres cotés en carré.

a² = b²+c²

'a' correspond à la 'distance' dans notre dessin, b = x2 - x1 et c = y2 - y1. Il faut encore changer la équation en

a = racine de (b²+c² )

Exprimant ceci en code, ça donnera la méthode suivante:

float distance(float x1, float y1, float x2, float y2){
float dx = x2 -x1;
float dy = y2 - y1;
float d = sqrt(dx*dx + dy*dy);
return d;
}

On aurait pu le faire plus simple, on utilisons la méthode dist(), mais cela nous a permis d'introduire à la trigonométrie.

système de coordonnées polaires

Jusqu'à présent nous avons abordé la programmation dans un système des coordonnées cartésiennes qui nous permet de décrire n'importe quel point dans un espace 2d (ou aussi 3d).

Mais nous pouvons imaginer aussi d'autres systèmes afin de s'orienter dans l'espace. Un autre est le système de coordonnées polaires. Au lieu d'écrire un point dans l'espace à travers l'abscisse (x) et l'ordonnée (y) à partir d'un point d'origine (0, 0) on peut aussi décrire un point à travers un angle qu'on nomme normalement du lettre grecque theta (θ )et une distance ou bien le rayon à partir d'un point d'origine..

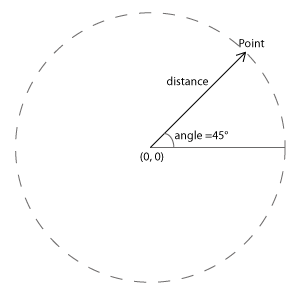
Convertion entre système polaire et cartésienne

Admettons nous voulons tourner un objet à 40px de distance autour d'un point. On pourrait le faire évidement avec la méthode rotate(), mais parfois ce n'est pas très pratique. Alors il faut convertir le point décrit dans le système polaire vers le système cartésienne. Si on superpose les deux systèmes on verra comment le faire.

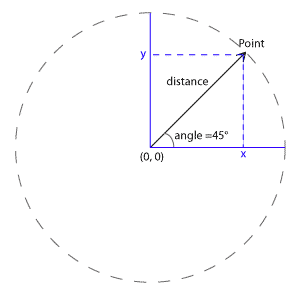
Si on regarde bien, la ligne de la distance, de x et y forment un triangle (il faut descendre y vers le bas). C'est là ou la trigonométrie nous aidera à calculer les distances de x et y. Rappelons nous qu'on peut calculer chaque coté d'un angle droite à partir d'un l'angle et d'une des cotés.

Étant donnée qu' il y a dans un triangle toujours la même proportion entre un angle donnée et ces trois cotés peu importe quel taille il a, il doit avoir des nombres qui expriment ces proportions. Ces nombres ont été appelé sinus cosinus et tangent. Par ailleurs on retrouve aussi cet même proportion constant dans un cercle et sa circonférence. Peut import la taille de cercle, la proportion entre la circonférence et son radian est de 2*PI.

Fonction trigonométrique

Voici les formules pour calculer les cotés d'un triangle.

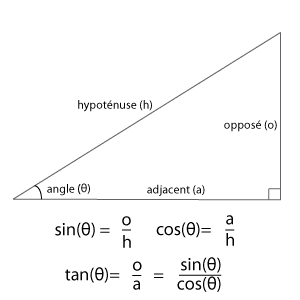
Alors le rayon représenta l'hypoténuse, l'opposé la distance sur y et l'adjacent la distance sur x.Dans un premier temps on réformule les fonctions sinus et cosinus.

o = sin( θ) * h
a = cos (θ)*h.

Et voilà, nous avons la formule pour calculer un point à partir d'un angle dans le système cartésien. Si les explications précédentes ont été obscure pour certains, il faut au moins retenir ce deux lignes.

x = cos (θ) * h
y = sin( θ) * h

Atan2

Un autre méthode très utile parmi les fonctions trigonométriques est atan2. Cette fonction, une modification du tangents permet de calculer l'angle entre le point d'origine et un autre point.

void draw() {
background(0);
float angle = atan2(mouseY, mouseX);
translate(mouseX, mouseY);
rotate(angle);
rectMode(CENTER);
rect( 0, 0, 40, 10);
}

 

void draw() {
background(0);
float angle=atan2( mouseY-height/2, mouseX-width/2);
translate(width/2, height/2);
println(mouseX);
rotate (angle);
rectMode(CENTER);
rect(0, 0, 40, 10);
}

Voici un exemple des yeux qui suivent la souris

Cercle

Avec les fonctions trigonométrique, on peut dessiner maintenant notre propre cercle, sans faire appelle à la fonction ellipse() pour ensuite imaginer d'autres forme à partir de ce formes ronds.

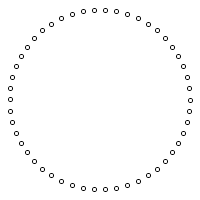
float x, y, r, angleStep, nbrPoint;// r = rayon 
int centreY, centreX;// pour placer le cercle au milieu
void setup() {
  size (200, 200);
  smooth();
  background(255);
  stroke(0);
  r= 90;
  centreX = width/2; 
  centreY = height/2;
  nbrPoint = 50; // les nombres des pt qu'on dessinera
  angleStep = TWO_PI/nbrPoint; 
  for (float angle = 0; angle < TWO_PI; angle+=angleStep) {
    x = centreX + cos(angle)*r;// centreX pour placer le circle au centre
    y = centreY + sin(angle)*r;
    ellipse(x, y, 4, 4);
  }
}

Spirale, rosace

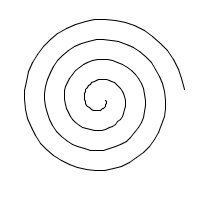
Ce n'est pas très intéressant, mais maintenant on peut commencer expérimenter. Avec quelques lignes de plus, on dessine un spirale, simplement en agrandissant le rayon progressivement. Les autres ligne de codes (last_x...) sont fait pour garder en mémoire les positions dans le boucle précédent. La boolean permet d'éviter de dessiner la première ligne qui reliera (x, y) avec (0, 0);

float x, y, last_x, last_y, r, rStep;// r = rayon
float angle, angleStep, nbrPoint; 
boolean firstTime=true;
int centreY, centreX;// pour placer le cercle au milieu
void setup() {
  size (200, 200);
  smooth();
  background(255);
  stroke(0);
  r= 5;
  rStep=0.4;
  centreX = width/2; 
  centreY = height/2;
  nbrPoint = 50; // les nombres des pt qu'on dessinera
  angleStep = TWO_PI/nbrPoint; 
  for (float angle = 0; angle<TWO_PI; angle+=angleStep) {
    r+=rStep;
    x = centreX + cos(angle)*r;// centreX pour placer le circle au centre
    y = centreY + sin(angle)*r;
    if (!firstTime) line(x, y, last_x, last_y);
    last_x = x;
    last_y = y;
    firstTime = false;
  }
}

 

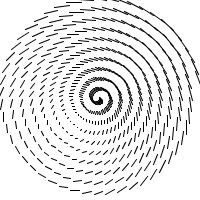
Maintenant on peut modifier les différents paramètres pour trouver d'autres formes. Simplement on changeant le rayon en utilisant le fonction sin (ou bien tan, le cos donne +/-) les mêmes résultat que sin) et quelques additions, multiplications on peut obtenir des dizaine des formes très différents. Voici quelques exemples, trouve les tiens, explore les fonctions trigonométriques d'une manière empirique!

 

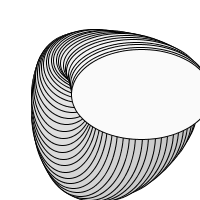
Cercle	spirale r+=ecartement	spirale ellipse à la place de line
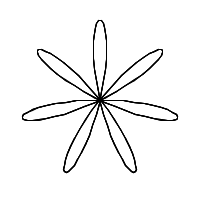
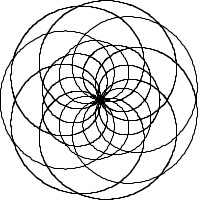
Spirale ligne(x+3, y,last_x, last-y)	Rosace r=90*sin(7*i)	Rosace complexe r=80*sin(0.7*i)+20

pour tester d'autres formes, regardez le site fooplot

voici les différents methodes pour dessiner les formes>>

Et encore une variation de la spirale par l'étudiant Guillaume Villeneuve >>

Voir ausi la Superformula

Ondulation

Avec ce code il n'est pas compliqué de dessiner des courbes. Il faut simplement avancé sur l'axe x ou y d'une manière linéaire. Voici un code très simple

int amplitude = 20;
int longeur_Onde = 10;
size (200, 200);
for (float i=0; i<2*TWO_PI; i+=.1){
float x= i*longeur_onde;
float y=sin(i) * amplitude;
point(x, y+100);
}

 

Ce qu'il faut connaître:

• être familier avec les classes
• connaître les bases de la trigonométrie

 

Exercice