Trans- form- ation/ Matrice tutorial de programmation en processing

Vera Molnar, Interruptions 1968-69

 

L'art, l'ordinateur et la transformation

 

L'art en général peut être considéré comme une transformation. Le sculpteur transforme sa matière brut (marbre, bronze, ...), le peintre transforme la toile avec la peinture, Duchamps a transformé les objets industriel en objet d'art et ainsi de suite. On attache à cette transformation une valeur symbolique, esthétique ou bien artistique. Nous attachons d'une manière générale a cette capacité de transformer la matière brut en valeur symbolique des qualités du génie, de l'inspiration, de la créativité. Un des pionnier de l'art algorithme, Michael Noll a tenté de vérifier à quel point un ordinateur est capable de reproduire la créativité humaine. Il a écrit un programme qui exécute des variations du tableau de Piet Mondrian : Composition avec Lignes, le chef d'oeuvre de l'art abstrait selon le renommé critique d'art Seuphor des années soixante. Noll a présenté par la suite l'originale et l'execution par ordinateur a une centaine de personnes. Sa sondage a révélé que la majorité ont préféré les tableaux de l'ordinateur.

P.Mondrian 1917, Composition with Lines ou M. Noll, 1964 Computer composition with Lines?

 

Référence et littérature

Michael Noll "Human or Machine: A Subjective Comparison of Piet Mondrian's ‘Composition with Lines’ and a Computer–Generated Picture"

Transformation

Par la suite, nous aborderons les principales méthodes de transformations. Dans Java/ Processing, il n'y a pas une méthode qui permet de transformer directement l'objet en question. Nous transformons en effet la matrice entière. Les deux méthodes principales s'appellent translate et le rotate.

 

translate ( )

L'origine (0, 0) de notre fenêtre est normalement en haut à gauche. Mais il y a des situations ou il est plus pratique de déplacer cet point d'origine. Pour le déplacer, Processing a une méthode translate( ) qui permet de changer le x et y de l'origine, ce qu'on appelle la transformation de la matrice:

translate(width/4, height/4);
rect(0, 0, 20, 20);

déplace l'origine de la fenêtre d'un quart de sa taille. Donc d'un coup, le rectangle n'est pas en haut à gauche, mais déplacé d'un quart en diagonal. Les translate() suivant vont s'aditionner, qui fait que le deuxième rectangle est déplacé d'un demie taille de la fenêtre. Par contre, le translate() fonction est annulé à chaque boucle dans le draw()

void draw( ){// n'a aucun effet de repetion de la fonction translate()
translate(width/4, height/4);
rect(0, 0, 20, 20);
translate(width/4, height/4);// s'additionne au translate() précédent
rect(0, 0, 20, 20);
}

     

 

rotate ( )

Mais à quoi bon si on peut mettre de width/4 directement à la place de x dans le rect ? La fonction translate est particulièrement utile avec la combinaison de rotate(), car cette fonction ne tourne pas un objet mais toute la matrice autour de son point d'origine. L'argument pour rotate() est un angle de rotation exprimer en radians. Nous sommes plutôt habitué d'exprimer des angles en degré. Mais en effet, le radians n'est pas complètement différents, simplement sa référence n'est pas 360° pour une rotation entier, mais 2*PI ('pi' est ce drôle de chiffre 3.14159... qui nous permet de calculer la surface d'un cercle, sa circonférence... à partir de son rayon). Sans comprendre tout pour l'instant, voyons simplement comment utiliser ce "radians" ce qui est très simple: si je veux tourner ma matrice de la moitié d'un cercle (360/2=180°) c'est PI, d'un quart(360/4=90°) PI/2 d'un dixième PI/5 etc.Le calcule de degré vers radians, c'est: angle°=PI/180 *angle et l'invers radians=180/PI*radians

Pour ceux à qui c'est vraiment trop compliqué, il y a la fonction radians qui transforme le degré en radians donc au lieu d'écrire (PI/4) ou bien (O.7853) j'écris radians(45) et j'obtiens le même résultat.

conversion entre degré et radians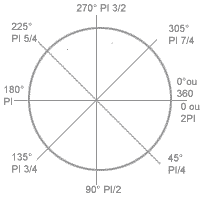

 

Mais revenons sur rotate. si j'écris

rotate(PI/4);
rect (width/2, height/2, 20, 20);

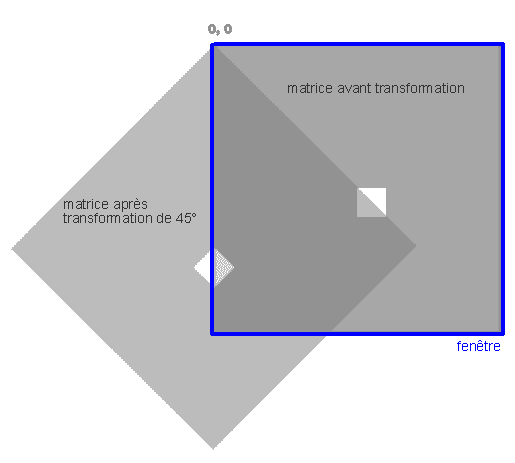
C'est la fenêtre qui s'est tourné de 45° de son point d'origine. Mais souvent on veut tourner plutôt un objet que la matrice, et c'est là ou la fonction translate ( ) est utile.Si on déplace l'origine de la fenêtre à son milieu ainsi le point de référence du rectangle dans son centre, la rotation s'effectue exactement autour du centre du rectangle dans le sens de l'aiguille.

rectMode(CENTER);
translate(width/2, height/2);
rotate(PI/4);
rect(0, 0, 20, 20);

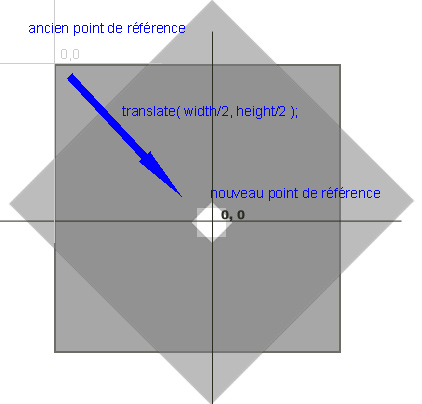
pushMatrix() / popMatrix

Imaginons on veut maintenant faire tourner deux rectangle l'un à coté de l'autre. Nous n'arriverons pas seulement avec les méthodes translate() et rotate(). Il faut faire recours à la notion de "matrix stack" . On entoure les transformations par les deux méthodes pushMatrix() et popMatrix(), ce qui limitent leurs validités à l'intérieur de ces deux méthodes.

float inc;
void draw(){
background(255);
rectMode(CENTER);
inc +=PI/30;
pushMatrix();// debut de la transformation du premier rectangle
translate(width/3, height/2);
rotate(inc);
rect(0, 0, 20, 20);
popMatrix();//fin de la transformation du premier rectangle
pushMatrix();// debut de la transformation du second rectangle
translate(width*2/3, height/2);
rotate(inc);
rect(0, 0, 20, 20);
popMatrix();//fin de la transformation du second rectangle
}

Ce qu'il faut connaître:

• Connaître les méthodes translate, rotate, pushMatrix et popMatrix

 

Exercice